Construction of atomic models of protein secondary structure elements

Author: Prof. Mariusz Jaskólski

Aims

Purpose of this practical

In this practical you will learn how to build elements of secondary structure of proteins. Doing this will help you to understand and remember the rules governing the stereochemistry of biomolecules. In particular, you will be able to understand the importance of hydrogen bonds.

For step 4 ...

For Step 5 you will need the following geometrical instruments:

• compass
• protractor
• ruler
• sharp pencil

Step 1

Familiarize yourself with the construction set

Fig. 1. The geometry of trans peptide group with bond distances in Å (black) and bond angles in degrees (red).

• The models are in CPK (Corey, Pauling, Koltun) convention, with the following color scheme: Carbon - black, Nitrogen - blue, Oxygen - red, Hydrogen - white.
• The Carbon atoms are in two variants: sp³ hybridization with 4 bonds arranged in tetrahedral manner (109.5 degrees apart), sp² hybridization with 3 bonds arranged trigonally in a plane (120 degrees apart). The Nitrogen atoms have sp² hybridization as they participate in electron delocalization over the entire peptide group. The Oxygen atoms are prepared for convenient formation of N-H...O hydrogen bonds.
• The model you are going to construct will have the following scale 1 Å is equivalent to 3 cm. The scale calculation includes the length of the stick ("bond") plus the radii of the connected atoms (2x5mm=10mm). The sticks representing Bonds have the following dimensions:
  Ca-C           about 1.51 Å  35 mm  (green)
Ca-N           about 1.46 Å  35 mm  (green)
Ca-Cb etc.     about 1.54 Å  35 mm  (green)
C-N            about 1.33 Å  30 mm  (gray) Peptide Bond
C=O            about 1.24 Å  27 mm  (red)
N-H, C-H etc.  about 1.0  Å  20 mm  (white)
NH...O         about 1.85 Å  45 mm  (white)

• In assembling the polypeptide main chain pay attention to the following topological aspects:
  • the main chain must have the correct atom sequence: ...-N-Ca-CO-...
  • the amino acids should have the L configuration
  • the peptide bonds should have the trans configuration (omega=180 degrees)
  • the phi and psi torsion angles of the main chain should have the appropriate Ramachandran values

Step 2

Construction of a polypeptide chain in beta (extended) conformation and of beta-sheets

1. Construct a pentapeptide AAAAA in extended conformation. Pay attention to the Ramachandran angles (phi about -120 degrees, psi about +120 degrees). Attach the Ala side chains (methyl groups -CH3 as you go).
2. Observe the alternating protrusion of the side chains above and below the planes of the peptide groups.
3. Construct a second beta-chain in a similar way.
4. Align the chains into an antiparallel beta-sheet; observe the regular pattern of the N-H...O/O...H-N hydrogen bonds formed between peptide groups from opposite chains.
5. Change the direction of one of the beta-chains to form a parallel beta-sheet; observe the changed pattern of H-bonding connections.
6. Observe the pleated character of the beta-sheets created in 4. and 5.

Step 3

Construction of an alpha helix and of a Leucine Zipper

1. Construct an octapeptide AAAAAAAA in alpha-helical conformation (helix 3.6₁₃). Pay attention to the Ramachandran angles (phi about -60 degrees and psi about -60 degrees). First, put together a poly-Gly chain; the Ala side chains (methyl groups -CH3) can be added later.
2. As soon as you have attached the N atom of the 4th residue of the growing polypeptide chain, connect it through an N-H...O hydrogen bond with the carbonyl (C=O) O atom of residue number 1. From this moment the polypeptide chain is no longer flexible (labile) and in fact becomes quite rigid (stable), and your work becomes a lot easier; observe the importance of hydrogen bonds in macromolecular structures.
3. Form the N-H...O hydrogen bonds as you go, whenever you have attached a new N-H group.
4. Change the side chains of residues n=1 and n+7=8 to leucine. Observe the nearly perfect alignment of these side chains along a line that is parallel to the helix axis. The misalignment is small: "0.2 residue". This is calculated from the 3.6x2=7.2 residues necessary for two complete turns of the 3.6₁₃ helix; with just 7 residues we are a small fraction (0.2) short of the perfect alignment.
5. Construct a second alpha-helix in a similar way.
6. Align the two helices in a parallel fashion and in such a way that the two bulky side chains at position n=1 face each other. Observe that for the n+7 residues to also face each other, the two helices must slightly turn around each other to bring these residues into alignment. This movement produces a superhelical twist to this two-helix motif. The result is a Left-handed superhelix (coiled coil). This motif is known as Lucine Zipper.

Step 4

Analyzing Leucine Zipper on paper

1. Draw the alpha helix in a projection along its axis, assuming that it is running towards you. The construction has been already started in Fig. 2 (left): the winding polypeptide chain climbs along the surface of a cylinder, and the perimeter of this cylinder is projected as a circle. The center of the circle represents the helix axis, seen in projection. Starting with residue numbered 1 (already shown), mark by small (numbered) circles the consecutive residues located on the perimeter of the cylinder.
2. Remembering that the numerical symbol of the alpha helix is 3.6₁₃, try to figure out the angular separation (in degrees) of the consecutive residues and, equally importantly, in which direction those angles should be measured. Mark minimum 22 residues. Try to figure out the sequences of numbers that correspond to those residues on the surface of the cylinder that are located on relatively straight lines parallel to the helix axis. Are there many solutions to this question, perhaps satisfying the condition of roughly parallel alignment with the helix axis in different degree?
3. In the next step, turn the cylinder from Fig. 2 (left) by 90 degrees as indicated by the arrow. You will get a different projection of the cylinder, as in Fig. 2 (right). Now the residue marked 1 is in the front and at the bottom. Fig. 2 (right) also contains a sketch of the helical line winding around the cylinder. Mark on this line the residues (small circles) according to their position in Fig. 2 (left). From all the drawn residues, select those that fulfill the rule: 1, (1 + 7) = 8, (8 + 7) = 15, ... Connect them with a line. Does this line have a helical twist? If yes, of what handedness?

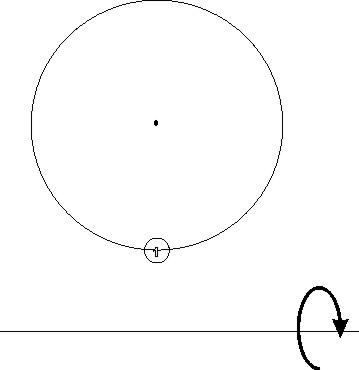
Fig. 2.

Homework

• A helical line making one full coil is drawn on the surface of a cylinder of diameter D and height (pitch) P. What is the length of this helical line?
• A wire of diameter d is wound in a single helical coil around a cylinder of diameter D and height (pitch) P. What is the length of this wire?

Step 5

Your Report

• Your Report from this practical, as from all other practicals, should be completed and sent to your tutor by email (szymon@amu.edu.pl) before the date of the following practical class.

back

Mariusz Jaskolski, 22.03.2009